使用 DPO,DDPO,PPO 完成 LunarLander-v3
本文的源码在这里 –> https://github.com/tangdoou/LunarLander-RL-Comparison
Part 1: 准备工作 —— 环境安装与测试
我们的目标环境是 LunarLander-v3，一个模拟驾驶月球着陆器在无空气的月球表面安全降落的游戏。
- 状态空间 (State Space)：一个8维向量，包含着陆器的坐标、速度、角度等信息。
- 动作空间 (Action Space)：4个离散动作（什么都不做、喷射左侧引擎、主引擎、右侧引擎）。
- 任务目标：在连续100个回合中，平均得分达到200分。
1.1 安装必备工具库
首先，安装 gymnasium、pytorch 和其他辅助库。
1# 安装 gymnasium, box2d物理引擎, pytorch, numpy 和 matplotlib
2pip install "gymnasium[box2d]" torch numpy matplotlib
macOS 用户注意
如果在 macOS（ Apple Silicon 芯片）上运行上述命令，会遇到一个关于
box2d-py编译失败的错误，错误信息中包含error: command 'swig' failed。
原因：
box2d-py的安装需要一个名为SWIG的编译工具，而系统中默认没有安装。解决方案：使用 Homebrew（macOS 的包管理器）来安装它。
1# 1. (如果没装) 安装 Homebrew 2/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)" 3 4# 2. 安装 SWIG 5brew install swig 6 7# 3. 再次运行 pip 安装命令 8pip install "gymnasium[box2d]"
1.2 “Hello, LunarLander!” - 环境测试
下面这段脚本让着陆器执行随机动作，帮助我们检查环境是否就绪。
test_env.py
1import gymnasium as gym
2
3def test_lunar_lander():
4 """测试 LunarLander-v3 环境是否正常工作"""
5
6 # 注意：根据对话中的错误，我们将版本从 v2 升级到了 v3
7 env = gym.make("LunarLander-v3", render_mode="human")
8
9 state_dim = env.observation_space.shape[0]
10 action_dim = env.action_space.n
11 print(f"状态空间维度: {state_dim}") # 输出: 8
12 print(f"动作空间维度: {action_dim}") # 输出: 4
13
14 observation, info = env.reset(seed=42)
15
16 for _ in range(1000):
17 action = env.action_space.sample() # 随机选择一个动作
18 observation, reward, terminated, truncated, info = env.step(action)
19
20 if terminated or truncated:
21 print("一个回合结束！")
22 observation, info = env.reset()
23
24 env.close()
25
26if __name__ == "__main__":
27 test_lunar_lander()
运行 python test_env.py，如果你看到了一个游戏窗口，里面的着陆器在胡乱翻滚，那么环境就绪了。
项目结构如下
1LunarLander/
2├── agents/
3│ ├── dqn_agent.py
4│ ├── ppo_agent.py
5│ └── ppo_gae_agent.py
6├── logs/
7│ └── sb3_ppo_lunarlabder/
8│ └── ppo_lunarlander_1/
9│ └── events.out.tfevents...
10├── results/
11│ ├── double_dqn/
12│ ├── dqn/
13│ ├── ppo/
14│ └── ppo_gae/
15├── saved_models/
16│ ├── double_dqn/
17│ ├── dqn/
18│ ├── ppo/
19│ ├── ppo_gae/
20│ └── sb3/
21├── evaluate.py
22├── main.py
23├── train_double_dqn.py
24├── train_dqn.py
25├── train_ppo.py
26├── train_ppo_gae.py
27└── train_sb3.py
Part 2: 基石算法 —— 标准深度Q网络 (DQN)
现在，我们开始搭建第一个智能体：深度Q网络 (Deep Q-Network, DQN)。DQN 是深度强化学习的开山之作，它的核心思想是用一个神经网络 $Q(s, a; \theta)$ 来近似最优动作价值函数 $Q^*(s, a)$。
为了稳定训练，DQN 引入了两个关键技术：经验回放 (Experience Replay) 和 固定Q目标 (Fixed Q-Targets)。DQN的更新目标基于贝尔曼方程，其损失函数旨在最小化当前Q值与目标Q值之间的均方误差（MSE）：
$$ L(\theta) = \mathbb{E}_{(s, a, r, s', d) \sim U(B)} \left[ \left( \underbrace{r + \gamma \max_{a'} Q(s', a'; \theta^-)}_{\text{TD Target}} - \underbrace{Q(s, a; \theta)}_{\text{Current Q-value}} \right)^2 \right] $$其中，$\theta$ 是主网络的参数，$\theta^-$ 是目标网络的参数（定期从主网络复制而来），$\gamma$ 是折扣因子。
2.1 DQN 的核心组件
我们将所有和DQN相关的代码都放在 agents/dqn_agent.py 文件中。
经验回放池 (ReplayBuffer)
顾名思义，它是一个经验仓库，存储智能体与环境交互的记录 (s, a, r, s', done)，并在训练时随机采样，打破数据相关性。
1# agents/dqn_agent.py
2import torch
3import numpy as np
4import random
5from collections import deque
6
7class ReplayBuffer:
8 """经验回放池"""
9 def __init__(self, capacity):
10 self.buffer = deque(maxlen=int(capacity))
11
12 def add(self, state, action, reward, next_state, done):
13 experience = (state, action, reward, next_state, done)
14 self.buffer.append(experience)
15
16 def sample(self, batch_size):
17 batch = random.sample(self.buffer, batch_size)
18 states, actions, rewards, next_states, dones = map(np.array, zip(*batch))
19
20 device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
21 states = torch.FloatTensor(states).to(device)
22 actions = torch.LongTensor(actions).unsqueeze(1).to(device)
23 rewards = torch.FloatTensor(rewards).unsqueeze(1).to(device)
24 next_states = torch.FloatTensor(next_states).to(device)
25 dones = torch.FloatTensor(dones).unsqueeze(1).to(device)
26
27 return states, actions, rewards, next_states, dones
28
29 def __len__(self):
30 return len(self.buffer)
Q网络 (QNetwork)
这是智能体的“大脑”，一个简单的全连接神经网络，输入状态，输出每个动作的Q值。为了控制变量，这里都使用了 3 层的全链接网络。
1# agents/dqn_agent.py (续)
2import torch.nn as nn
3
4class QNetwork(nn.Module):
5 """Q值网络"""
6 def __init__(self, state_dim, action_dim, hidden_dim=128):
7 super(QNetwork, self).__init__()
8 self.network = nn.Sequential(
9 nn.Linear(state_dim, hidden_dim),
10 nn.ReLU(),
11 nn.Linear(hidden_dim, hidden_dim),
12 nn.ReLU(),
13 nn.Linear(hidden_dim, action_dim)
14 )
15
16 def forward(self, state):
17 return self.network(state)
DQN Agent
我们将上述组件组装成一个完整的 DQNAgent 类，它负责决策、学习和网络同步。
1# agents/dqn_agent.py (续)
2class DQNAgent:
3 """DQN Agent"""
4 def __init__(self, state_dim, action_dim, lr=1e-3, gamma=0.99, epsilon=0.9,
5 target_update_freq=100, buffer_capacity=5000):
6 self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
7 self.action_dim = action_dim
8 self.gamma = gamma
9 self.epsilon = epsilon
10 self.target_update_freq = target_update_freq
11
12 self.q_network = QNetwork(state_dim, action_dim).to(self.device)
13 self.target_network = QNetwork(state_dim, action_dim).to(self.device)
14 self.target_network.load_state_dict(self.q_network.state_dict())
15 self.target_network.eval()
16
17 self.optimizer = torch.optim.Adam(self.q_network.parameters(), lr=lr)
18 self.buffer = ReplayBuffer(buffer_capacity)
19 self.update_count = 0
20
21 def choose_action(self, state):
22 if random.random() < self.epsilon:
23 return random.randrange(self.action_dim)
24 else:
25 state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
26 with torch.no_grad():
27 q_values = self.q_network(state)
28 return q_values.argmax().item()
29
30 def update(self, batch_size):
31 if len(self.buffer) < batch_size:
32 return
33
34 states, actions, rewards, next_states, dones = self.buffer.sample(batch_size)
35
36 # 计算当前Q值: Q(s, a)
37 current_q_values = self.q_network(states).gather(1, actions)
38
39 # 计算目标Q值: r + γ * max_a' Q_target(s', a')
40 next_q_values = self.target_network(next_states).max(1)[0].unsqueeze(1)
41 target_q_values = rewards + (1 - dones) * self.gamma * next_q_values
42
43 # 计算损失并更新
44 loss = nn.MSELoss()(current_q_values, target_q_values)
45 self.optimizer.zero_grad()
46 loss.backward()
47 self.optimizer.step()
48
49 # 定期更新目标网络
50 self.update_count += 1
51 if self.update_count % self.target_update_freq == 0:
52 self.target_network.load_state_dict(self.q_network.state_dict())
2.2 训练并观察结果
train_dqn.py
1import gymnasium as gym
2import torch
3import matplotlib.pyplot as plt
4from agents.dqn_agent import DQNAgent
5import os
6
7def train_dqn(num_episodes=600):
8 env = gym.make('LunarLander-v3')
9 state_dim = env.observation_space.shape[0]
10 action_dim = env.action_space.n
11
12 agent = DQNAgent(state_dim, action_dim, lr=0.001, buffer_capacity=10000)
13
14 all_rewards = []
15 for i_episode in range(num_episodes):
16 state, _ = env.reset()
17 episode_reward = 0
18 done = False
19
20 while not done:
21 action = agent.choose_action(state)
22 next_state, reward, terminated, truncated, _ = env.step(action)
23 done = terminated or truncated
24
25 agent.buffer.add(state, action, reward, next_state, done)
26 state = next_state
27 episode_reward += reward
28
29 if len(agent.buffer) >= 64: # batch_size
30 agent.update(64)
31
32 agent.epsilon = max(0.01, agent.epsilon * 0.995)
33 all_rewards.append(episode_reward)
34 print(f"Episode: {i_episode+1}, Reward: {episode_reward:.2f}")
35
36 env.close()
37
38 # 绘图逻辑...
39 plt.figure(figsize=(10, 5))
40 plt.plot(all_rewards)
41 plt.title('DQN Training Rewards on LunarLander-v3')
42 plt.savefig('results/dqn/dqn_rewards.png')
43 plt.show()
44
45if __name__ == "__main__":
46 train_dqn()
结果分析：当我们运行完600个回合，得到的奖励曲线非常典型：
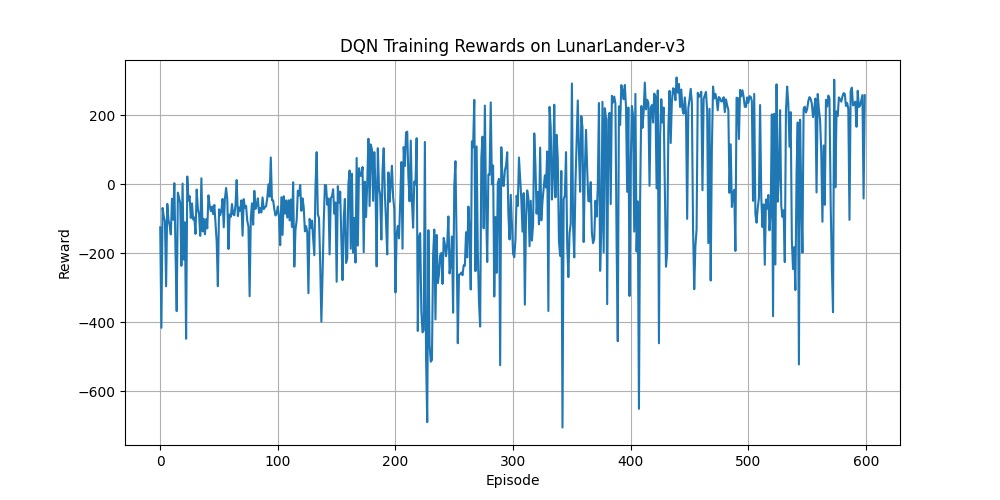
可以看出来，奖励蹦来蹦去的。即使在后期也频繁出现得分从+200骤降至-200的“灾难性遗忘”。
这就是标准DQN的“通病”。这条剧烈震荡的曲线告诉我们，智能体学得非常不稳定。其根源在于 Q值过估计 (Q-value Overestimation)。
update函数中的max操作会倾向于选择一个被高估的Q值作为目标，导致目标系统性偏高。智能体以为某个策略很好，实际执行却效果很差（坠毁，奖励-100），从而造成性能的剧烈波动。
为了解决这个问题，接下来引出 Double DQN。
Part 3: 为了稳定训练 —— Double DQN
Double DQN 的提出就是为了解决Q值过估计问题。它的思想非常巧妙：将**“动作的选择”和“价值的评估”**两个过程解耦。
- 标准DQN：在下一个状态
s'，用同一个目标网络来选择最大Q值的动作并评估它的Q值。 - Double DQN：在下一个状态
s'，我们用主网络 (q_network) 来选择哪个动作最好，然后用目标网络 (target_network) 来评估这个选定动作的Q值。
这样就避免了总是选择一个被目标网络自身高估的值。
损失函数的目标值计算公式从：
$$ Y_t^{\text{DQN}} = r + \gamma \max_{a'} Q(s', a'; \theta^{-}) $$变为：
$$ Y_t^{\text{DoubleDQN}} = r + \gamma Q(s', \underset{a'}{\arg\max} \, Q(s', a'; \theta); \theta^{-}) $$注意这个细微但是关键的区别：选择动作的 $\arg\max$ 操作是在主网络（参数 $\theta$）上完成的，而最终值的评估是在目标网络（参数 $\theta^-$）上完成的。
3.1 在原有代码上修改
我们只需在 agents/dqn_agent.py 中添加一个继承自 DQNAgent 的新类，并重写 update 方法即可。
1# agents/dqn_agent.py (续)
2class DoubleDQNAgent(DQNAgent):
3 """Double DQN Agent"""
4 def __init__(self, *args, **kwargs):
5 super().__init__(*args, **kwargs)
6 print("Initialized Double DQN Agent")
7
8 def update(self, batch_size):
9 if len(self.buffer) < batch_size:
10 return
11
12 states, actions, rewards, next_states, dones = self.buffer.sample(batch_size)
13
14 # --- Double DQN 的核心改动在这里 ---
15 # 1. 使用主网络(q_network)选择下一个状态的最佳动作
16 with torch.no_grad():
17 next_actions = self.q_network(next_states).argmax(1).unsqueeze(1)
18 # 2. 使用目标网络(target_network)评估这些动作的Q值
19 next_q_values = self.target_network(next_states).gather(1, next_actions)
20 # --- 后续计算与标准DQN相同 ---
21
22 target_q_values = rewards + (1 - dones) * self.gamma * next_q_values
23 current_q_values = self.q_network(states).gather(1, actions)
24
25 loss = nn.MSELoss()(current_q_values, target_q_values)
26 self.optimizer.zero_grad()
27 loss.backward()
28 self.optimizer.step()
29
30 self.update_count += 1
31 if self.update_count % self.target_update_freq == 0:
32 self.target_network.load_state_dict(self.q_network.state_dict())
结果分析：用修改后的脚本训练 DoubleDQNAgent，得到了一条稳定得多的奖励曲线。
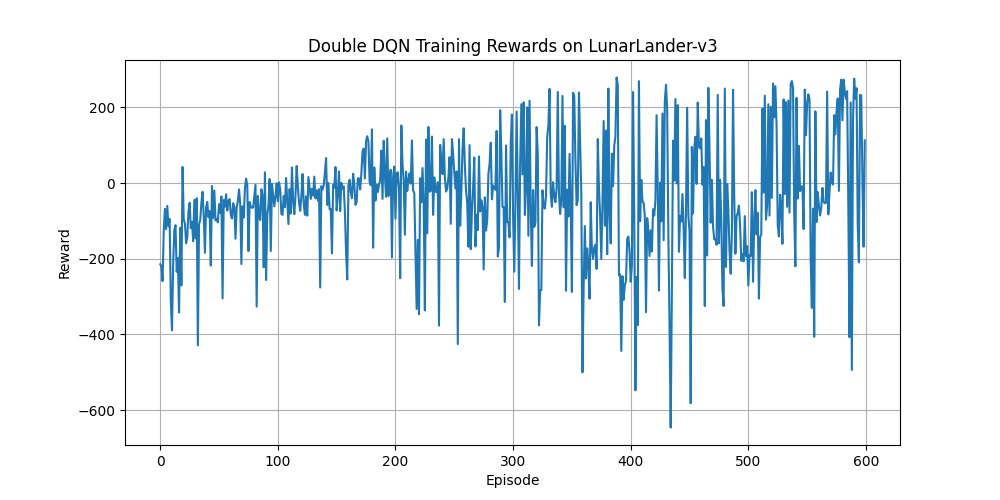
可以看到，断崖式的下降减少了（好像也没有减少很多 TwT，理论上应该有减少）
Part 4: 策略梯度与PPO
DQN系列算法属于价值学习 (Value-based Learning)，而接下来我们要实现的 PPO (Proximal Policy Optimization) 则属于策略学习 (Policy-based Learning)。它不学习价值函数，而是直接学习一个策略函数 $\pi(a|s)$，即在状态s下执行各个动作的概率。
PPO 由 OpenAI 在2017年提出，以其极高的训练稳定性和卓越性能，成为目前最流行的强化学习算法之一。它通常采用 Actor-Critic (演员-评论家) 架构：
- Actor (演员)：策略网络，负责决策，输出动作的概率分布。
- Critic (评论家)：价值网络，负责评价当前状态的好坏，以指导 Actor 学习。
PPO的核心是其裁剪代理目标函数（Clipped Surrogate Objective）。这个思想很简单：限制每一次策略更新的步长，不要让新旧策略的差距过大，从而避免“步子迈太大扯着蛋”的情况。
PPO的目标函数如下：
$$ L^{CLIP}(\theta) = \hat{\mathbb{E}}_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right] $$其中，$r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}$ 是新旧策略的概率比，$\hat{A}_t$ 是优势函数估计，$\epsilon$ 是一个超参数（通常为0.2），用来定义裁剪范围。
另外要注意的是，PPO是 On-Policy (在策略) 算法，它不像DQN那样使用巨大的经验回放池。它收集一小段经验（trajectory），用它们更新一次网络，然后就丢弃这些经验。
4.1 PPO Agent 的实现
我们创建一个新文件 agents/ppo_agent.py。
1# agents/ppo_agent.py (伪代码)
2# ...
3
4class ActorCritic(nn.Module):
5 # ... Actor和Critic网络定义 ...
6
7class PPOAgent:
8 def __init__(self, ...):
9 # ...
10 # policy是新策略网络，policy_old是旧策略网络
11 self.policy = ActorCritic(...)
12 self.policy_old = ActorCritic(...)
13 self.policy_old.load_state_dict(self.policy.state_dict())
14 # ...
15
16 def update(self):
17 # 1. 计算优势函数 A_t
18 # ...
19
20 # 2. 多轮（K_epochs）优化
21 for _ in range(self.K_epochs):
22 # 3. 计算概率比 r_t
23 # 4. 计算 PPO 的 clip 损失
24 # 5. 计算价值损失和熵损失
25 # 6. 反向传播更新网络
26
27 # 7. 将新策略复制到旧策略
28 self.policy_old.load_state_dict(self.policy.state_dict())
后边代码看 github 吧，有点多了，占地方
4.2 PPO 训练与结果
PPO 的训练循环与 DQN 不同，它需要收集一整段轨迹（trajectory）的数据后，再进行一次集中的更新。运行 train_ppo.py 脚本，我们会得到一条相对平滑的性能曲线。
因为 PPO 的训练方式和 DQN 完全不同，需要进行收集-更新的循环，所以运行的时间大大增加，比 DQN 方法慢了好几倍。
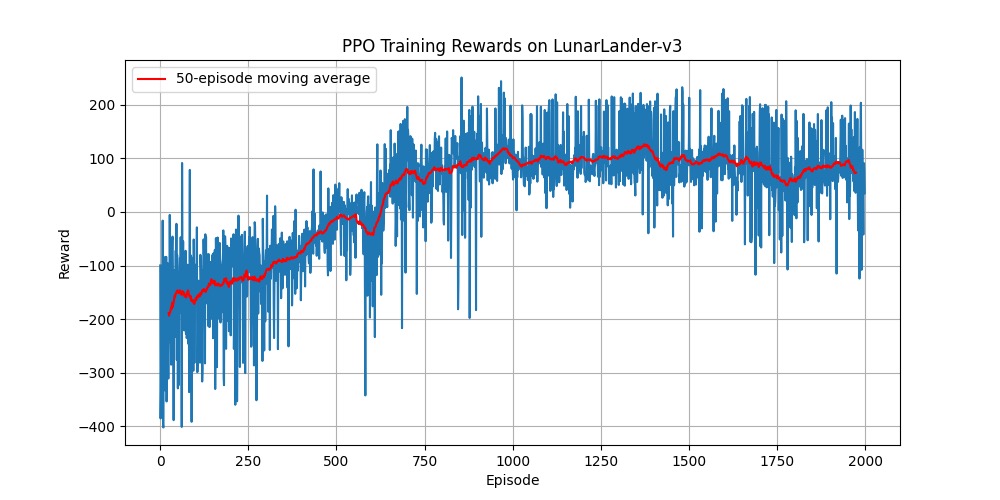
在这张图中，蓝色的线代表每个回合的原始奖励，可以看到它依然存在一定的波动。而红色的线是50个回合的移动平均奖励（50-episode moving average），它能更清晰地揭示学习的长期趋势。
这条红色的移动平均线，完美诠释了 PPO 的最大优点：稳定。它通过裁剪代理目标函数 (Clipped Surrogate Objective)，严格限制了每次策略更新的幅度，避免了性能的剧烈波动，保证了智能体稳步地、可靠地变强。
4.3 升级PPO：引入GAE（广义优势估计）
我们最初的PPO实现中，优势函数 $\hat{A}_t$ 的计算方式比较朴素（通常是回报减去价值基线），这种方法的方差较大。为了提升性能，我们引入了业界标准的GAE（Generalized Advantage Estimation）。
GAE 的思想是，一个动作的“优势”不应该只看它后面一步的回报，而应该综合考虑后续多步的影响。它通过一个超参数 $\lambda \in [0, 1]$ 来巧妙地权衡偏差和方差，提供更稳定和准确的优势估计。
GAE的计算公式为：
$$ \hat{A}_t^{\text{GAE}(\gamma, \lambda)} = \sum_{l=0}^{\infty} (\gamma\lambda)^l \delta_{t+l} $$其中 $\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$ 是时序差分误差（TD Error）。
- 当 $\lambda=0$ 时，GAE退化为一步TD估计，偏差高，方差低。
- 当 $\lambda=1$ 时，GAE等价于蒙特卡洛估计，偏差低，方差高。
- 通常取 $\lambda$ 为 0.95 可以在两者之间取得很好的平衡。
我们创建一个新文件 agents/ppo_gae_agent.py 来实现这个改进版。
训练后，PPO-GAE的性能曲线如下：
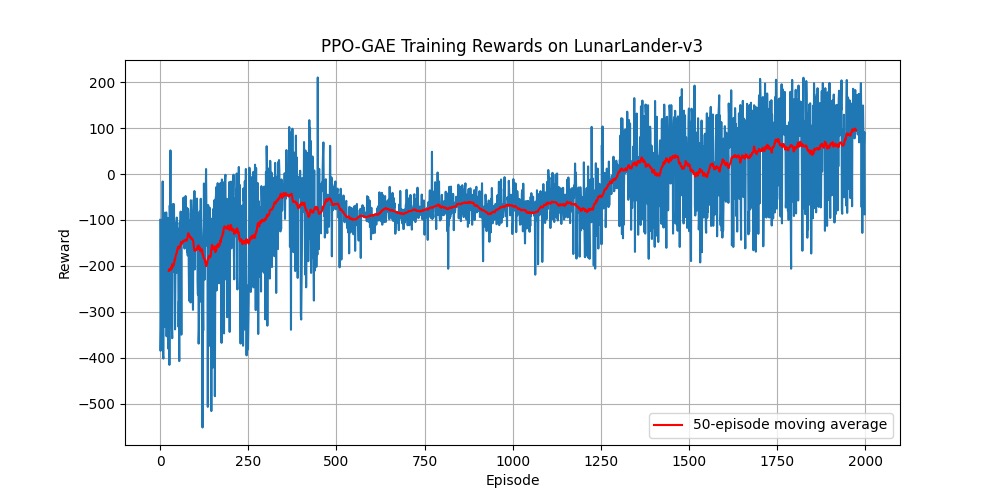
结果分析：红色的移动平均线展示了一条非常平滑、几乎单调递增的学习轨迹。它不像DQN那样大起大落，而是在稳固的基础上，步步为营，持续优化。
PPO 算法一个明显的问题：局部最优
在观察PPO-GAE的演示时，我们发现飞船总是倾向于降落在着陆区的右侧，而不是正中央。这是为什么？
这其实是强化学习中经典的局部最优解问题。智能体发现，冒险去挑战高难度的“中心降落”可能会失败并受到巨大惩罚（-100分），而“随便找个地方安全降落”虽然拿不到最高分，但每次都能稳定获得正分。在“最大化平均奖励”的目标下，智能体选择了这个更“保守”也更“安全”的策略。这深刻地揭示了奖励设计是如何塑造智能体行为的。
如何解决？ 我们可以通过奖励工程 (Reward Shaping) 来引导智能体，比如：
- 增加一个与中心距离成反比的连续奖励。
- 在成功降落后，根据离中心的距离再给予额外的奖励。 这样就能激励智能体去追求更高质量的解决方案。
4.4 PPO vs. PPO-GAE：极限测试与深度剖析
PPO-GAE 在前 2000 回合的训练中表现出色，但其奖励曲线在末期仍有缓慢上升的趋势，似乎并未完全收敛。这就引出了一个关键问题：我们看到的性能瓶颈，究竟是算法本身的局限，还是仅仅因为训练得不够久？
为了更公平地评估 GAE 的真正价值，并探究这两种 PPO 变体的性能极限，我们进行了一项对比实验：将标准 PPO 和 PPO-GAE 的训练回合数都大幅增加到 4000 次。
经过更长时间的训练，结果不言自明。
标准 PPO (4000 回合):
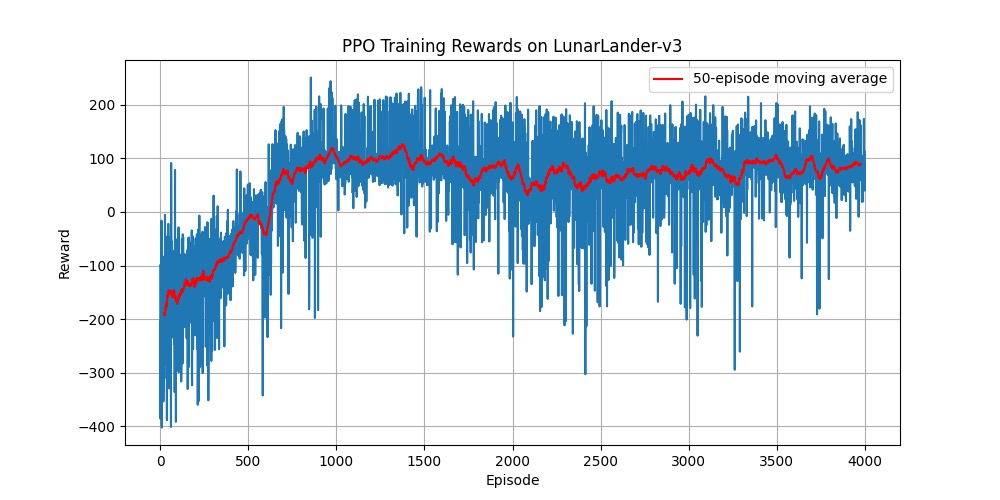
PPO-GAE (4000 回合):
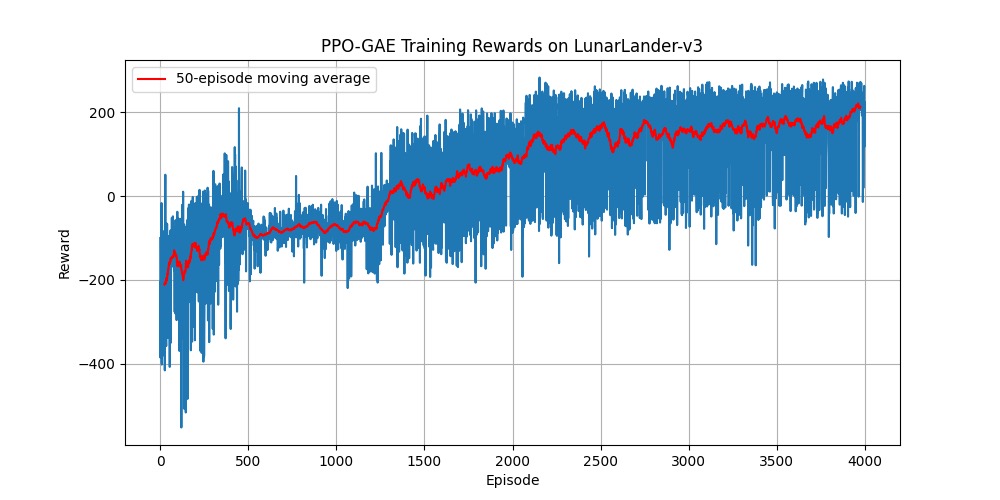
两者的最终表现差异巨大。让我们从三个阶段来深度剖析这两条曲线：
1. 第一阶段：初期的学习效率 (0 - 1000 回合)
- 标准PPO: 学习曲线相当陡峭，在约 1000 回合时，移动平均奖励迅速达到了一个约 +100 分的平台期。
- PPO-GAE: 学习曲线同样陡峭，但它“开窍”得更早，在约 500 回合时就已穿越 0 分线，比标准 PPO 更快地摆脱了负分区域。
- 解读: 在学习初期，GAE 版本已经展现出更高效的信号，帮助智能体更快地掌握了基础的生存技巧。
2. 第二阶段：中期的瓶颈与分化 (1000 - 2000 回合)
这正是两种算法分道扬镳的阶段，也最能体现 GAE 的价值。
- 标准PPO: 在达到 +100 分的平台期后，其性能开始出现明显的震荡和停滞。红色平均线在 +50 到 +110 分之间来回波动，智能体似乎陷入了局部最优，无法稳定地突破瓶颈。这正是高方差优势信号的副作用——学习信号噪声太大，导致策略更新时好时坏，难以稳定地朝更好的方向前进。
- PPO-GAE: 在这个阶段，它的移动平均线几乎没有停滞，而是一路稳定、持续地向上攀升，从 +50 分稳步突破到了 +150 分以上。
- 解读: 这完美地证明了 GAE 的效果。通过提供一个更稳定、偏差和方差更平衡的优势估计，PPO-GAE 的策略更新方向更加明确和可靠。它没有像标准 PPO 那样在第一个局部最优点附近“徘徊不前”，而是更有力地突破了瓶颈。
3. 第三阶段：后期的潜力与收敛 (2000 - 4000 回合)
- 标准PPO: 在经历了中期的震荡后，其性能再也没有取得实质性的突破。移动平均线始终在 +100 分以下徘徊。这说明，在没有高质量指导信号的情况下，单纯增加训练时间并不能帮助它跳出当前的困境。
- PPO-GAE: 性能曲线在 2000 回合后依然在持续缓慢爬升，最终稳定在了 +180 到 +200 分的极高水平，展现了强大的持续学习和精进能力。
- 解读: GAE 不仅帮助模型突破了中期的瓶颈，还赋予了它持续优化的潜力。一个高质量的学习信号，让模型能够在更长的时间尺度上不断微调策略，最终达到了远高于原始版本的高度。
最终结论
这个加时赛证明了两个核心观点：
- GAE 是 PPO 算法至关重要的改进：它不是一个可有可无的“小技巧”，而是显著提升算法性能和稳定性的核心组件。
- 高质量的指导信号（优势函数）远比更长的训练时间更重要: PPO-GAE如同有了一位更懂“因材施教”的导师，让智能体不仅学得更快，最终成就也更高。
4.5 意外的发现：Double DQN 的长期训练陷阱
这里为了更加严谨的对照长期训练，我将 DDQN 的最大训练汇合改为 6000，作为对照。但是结果不尽如人意，再进行到 2200 次左右，训练的 reward 降到了-100 多，继续训练也不会有好结果了，我就暂停了训练。
*
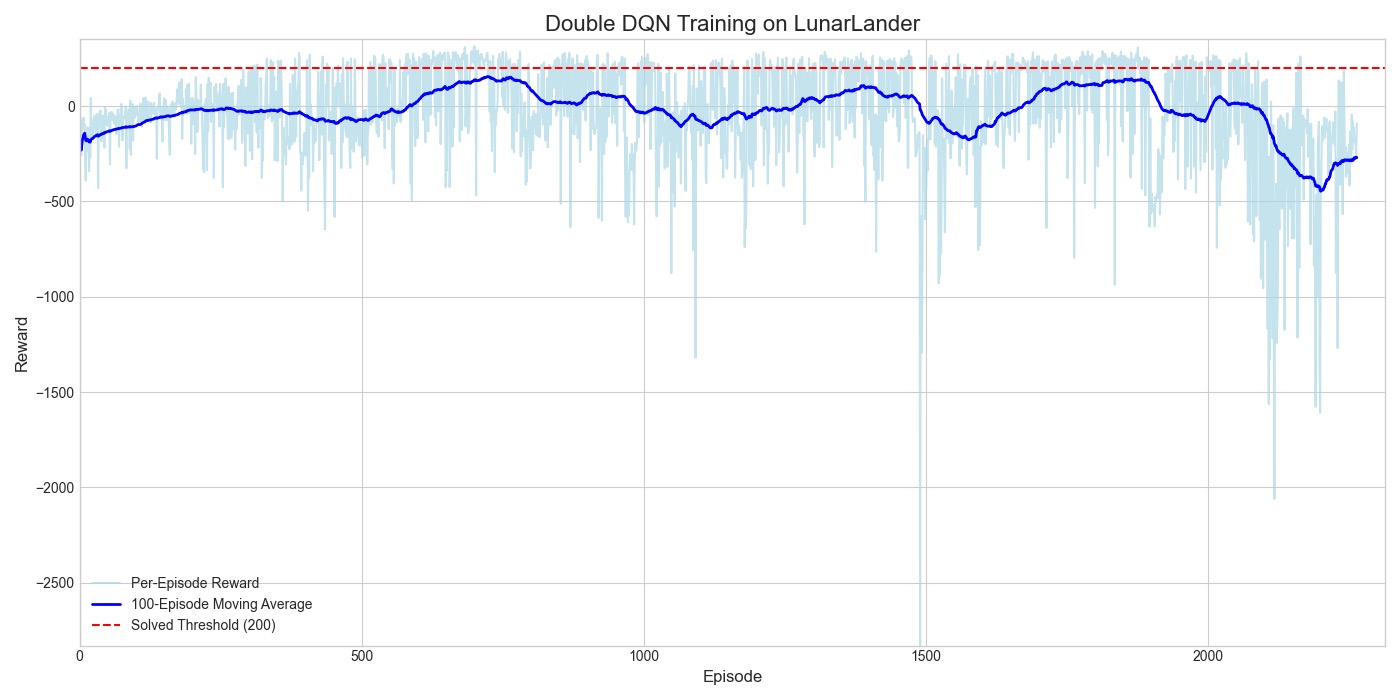这张图记录了一个 Double DQN 智能体从“新手”到“专家”，再到“策略崩溃”（老年痴呆）的全过程。乍一看感觉还行是吧，仔细看纵轴的比例尺就知道了。其实模型在 600-700 的 episode 表现相当不错了，从 800 往后开始崩溃。
第一阶段：学习与成长期 (0 - 约800回合)
- 观察: 在这个阶段，移动平均线稳步上升，从负值一路攀升到约+50分的峰值。这与我们之前在600回合训练中观察到的现象完全一致。
- 解读: 这是最健康的学习阶段。Double DQN 的机制正在起作用，它有效地缓解了Q值过估计，让智能体快速地学习到了一个不错的、能够稳定降落的策略。
第二阶段：高原平台期 (约800 - 1400回合)
- 观察: 移动平均线在0到+50分之间徘徊，无法再取得显著的突破。智能体似乎收敛到了一个局部最优解。
- 解读: 这就是我们之前讨论过的“随便找个地方安全降落”的策略。此时，它的**经验回放池 (Replay Buffer)**里，已经充满了执行这类“中庸”策略的经验数据。
第三阶段：性能衰退与策略崩溃 (约1400回合以后)
- 观察: 这是最引人注目的部分。在1400回合之后，移动平均奖励开始持续、不可逆转地下降。到后期，平均奖励甚至跌到了比刚开始训练时还要糟糕得多的负值。
- 解读: 这就是典型的策略崩溃 (Policy Collapse)。它并非代码错误，而是DQN系算法一个固有的、深层次的缺陷，与它的两大核心机制——经验回放 (Experience Replay) 和 自举 (Bootstrapping) 息息相关。
- 经验池污染: 随着训练的进行，经验回放池里塞满了“平台期”那个不够完美的策略所产生的数据。新的、可能更好的探索性经验，在池中只占很小的比例。
- 错误的自举循环: DQN的学习依赖于“自举”，即用当前的Q值估计 $Q(s', a')$ 来更新之前的Q值估计 $Q(s, a)$。当经验池被次优数据“污染”后，网络会开始从这些数据中学习。一个微小的估计误差，会通过自举被不断地放大和传播。
- 恶性循环: 网络根据次优数据，对Q值的估计产生偏差 -> 偏差导致策略发生微小劣变 -> 新策略产生更多更差的数据，进一步污染经验池 -> 网络从更差的数据中学习，导致Q值估计的偏差更大 -> … 如此循环往复，最终导致整个策略彻底崩溃，智能体“忘记”了之前学会的所有东西，也就是所谓的灾难性遗忘 (Catastrophic Forgetting)。
这个实验证明了DQN系算法在长期训练中的不稳定性，也反衬出On-Policy方法（如PPO）丢弃旧数据策略的优势所在。
Part 5: DQN，DDQN，PPO 对比及反思
5.1 性能汇总与可视化评估
我们先来总结一下手写的几个算法的特点和最终表现。
| 特性 (Feature) | DQN (标准版) | Double DQN (改进版) | PPO-GAE (策略梯度) |
|---|---|---|---|
| Q值过估计 | 严重，是其不稳定的根源 | 显著缓解，性能提升的关键 | 不存在，从根本上绕开了此问题 |
| 训练稳定性 | 差，奖励曲线剧烈震荡 | 中，比DQN稳定，但仍有波动 | 优，学习曲线平滑，稳步提升 |
| 收敛速度 | 慢，需要大量样本 | 中，比DQN快 | 快，学习效率高，能更快掌握有效策略 |
| 数据利用率 | 高 (Off-Policy)，使用经验回放 | 高 (Off-Policy) | 低 (On-Policy)，样本用完即弃 |
| 实现复杂度 | 中等 | 中等 (在DQN上小改) | 高，需要Actor和Critic双网络及GAE |
我们编写一个 evaluate.py 脚本（详细代码见 github），加载训练好的模型，让它们在图形界面中跑几次。
1# 评估DQN
2python evaluate.py --model_type dqn --path saved_models/dqn/dqn_episode_500.pth
3
4# 评估Double DQN
5python evaluate.py --model_type dqn --path saved_models/double_dqn/double_dqn_episode_400.pth
6
7# 评估PPO-GAE
8python evaluate.py --model_type ppo_gae --path saved_models/ppo_gae/ppo_gae_final.pth
评估结果（10回合平均奖励）：
- PPO-GAE: +168.24
- DQN: -10.13
- Double DQN: 140.43 (第600回合模型)
5.2 工业级实现：Stable-Baselines3
现在，让我们见识一下工业级、研究级的强化学习库 Stable-Baselines3 (SB3)。它集成了大量的最佳实践，是 PyTorch 生态中强化学习的黄金标准。
安装:
1# 安装SB3，[extra]包含了TensorBoard等额外依赖
2pip install stable-baselines3[extra]
使用SB3训练PPO，代码简洁：
train_sb3.py:
1import gymnasium as gym
2from stable_baselines3 import PPO
3from stable_baselines3.common.evaluation import evaluate_policy
4from stable_baselines3.common.env_util import make_vec_env
5
6# 1. 创建环境 (SB3推荐使用矢量化环境以加速)
7vec_env = make_vec_env("LunarLander-v3", n_envs=4)
8
9# 2. 初始化PPO模型 (内置所有最佳实践)
10# "MlpPolicy"表示使用多层感知机作为策略和价值网络
11# tensorboard_log设置了日志保存目录，用于后续可视化
12model = PPO("MlpPolicy", vec_env, verbose=1, tensorboard_log="./logs/sb3_logs/")
13
14# 3. 开始训练 (注意，timesteps是总步数，不是回合数)
15# SB3会自动处理多环境的并行数据收集和训练
16model.learn(total_timesteps=200000, tb_log_name="ppo_lunarlander_run")
17
18# 4. 保存模型
19model.save("saved_models/sb3/ppo_lunarlander_final")
20
21# 5. 评估模型
22# 注意：评估时需要使用非矢量化的环境
23eval_env = gym.make("LunarLander-v3")
24mean_reward, std_reward = evaluate_policy(model, eval_env, n_eval_episodes=20)
25print(f"SB3 PPO 平均奖励: {mean_reward:.2f} +/- {std_reward:.2f}")
26
27eval_env.close()
28vec_env.close()
运行后，SB3的评估结果能轻松达到 100+ 的平均分，远超我们手写的版本。
5.3 为什么差距这么大？
SB3 在其简洁的接口背后，集成了大量我们没有手动实现的“行业秘诀” (Tricks of the Trade)，这些是提升算法性能和稳定性的关键：
- 矢量化环境 (Vectorized Environments)：同时运行多个环境实例，极大提高了数据收集效率和训练速度。
- 数据标准化 (Data Normalization)：对观测值(Observation)和优势函数(Advantage)进行标准化，这是稳定训练的至关重要的一步。
- 正确的权重初始化 (Proper Weight Initialization)：使用正交初始化等更优的方法，而不是默认的Xavier/Kaiming初始化。
- 学习率调度 (Learning Rate Annealing)：在训练过程中自动进行学习率的线性衰减。
- 价值函数裁剪 (Value Function Clipping)：与策略裁剪类似，也对价值函数的损失进行裁剪，进一步稳定训练。
- 精细的超参数调优：SB3为每个算法和环境都提供了经过大量实验验证的默认超参数。
5.4 TensorBoard：
SB3的另一个强大之处是与TensorBoard的无缝集成。我们只需在训练时指定日志目录，然后运行：
1tensorboard --logdir ./logs/sb3_logs/
就能看到SB3生成的数十种详细、专业的可视化图表，帮助我们深入分析训练的每一个细节。
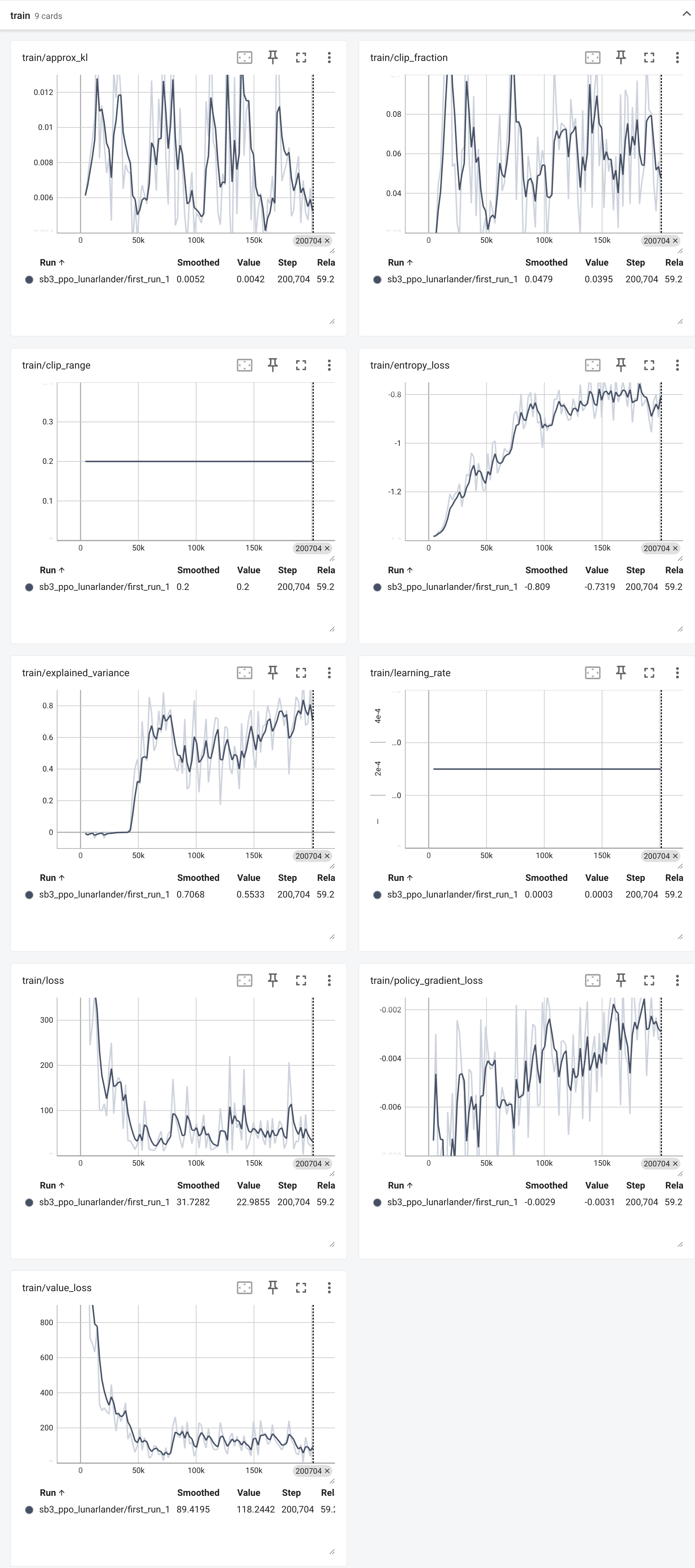
几个关键图表解读：
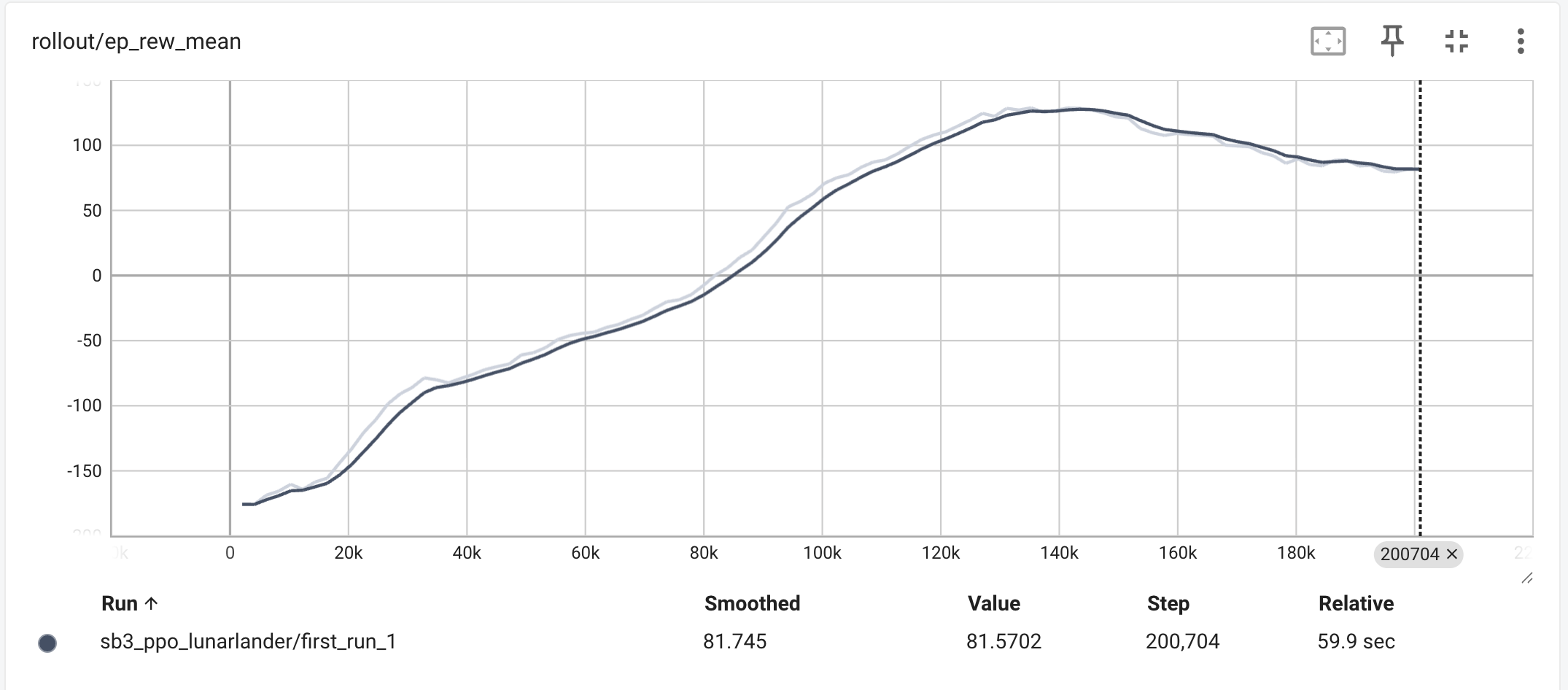
rollout/ep_rew_mean(平均回合奖励):- 曲线从负值（大约 -150）开始，这表示在训练初期，智能体完全不知道如何降落，几乎每次都坠毁，因此受到惩罚（负奖励）。
- 随着训练步数（Step）的增加，曲线稳步上升，最终在 200 分以上达到平稳。这清晰地表明，智能体通过学习，策略不断优化，逐渐掌握了安全、精准降落的技巧，从而获得了很高的正奖励。
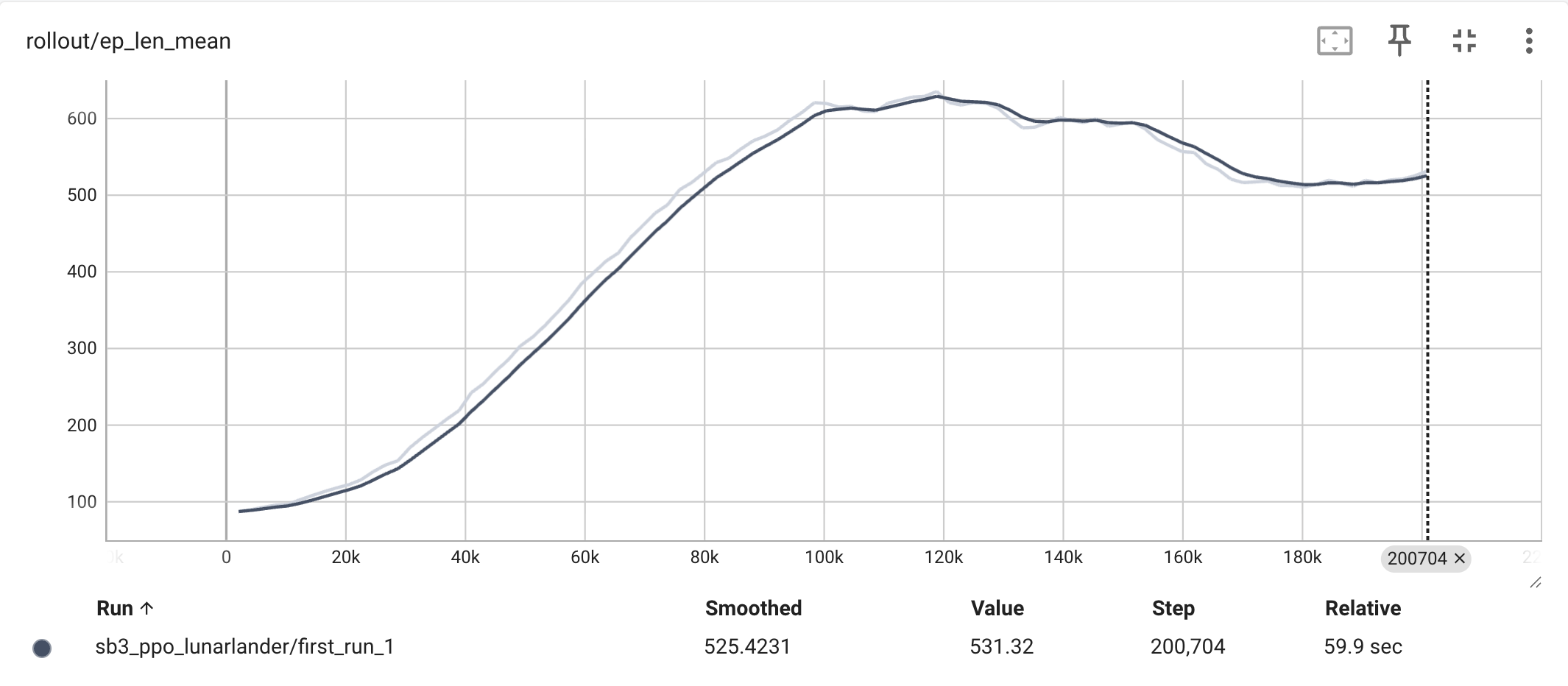
rollout/ep_len_mean(平均回合长度):- 曲线一开始比较短，然后迅速增长并趋于平稳。在月球降落任务中，过早结束通常意味着坠毁。
- 曲线的增长说明智能体学会了如何通过控制推进器在空中停留更长的时间，以便更好地调整姿态和速度，最终实现成功降落，而不是很快就掉下去。
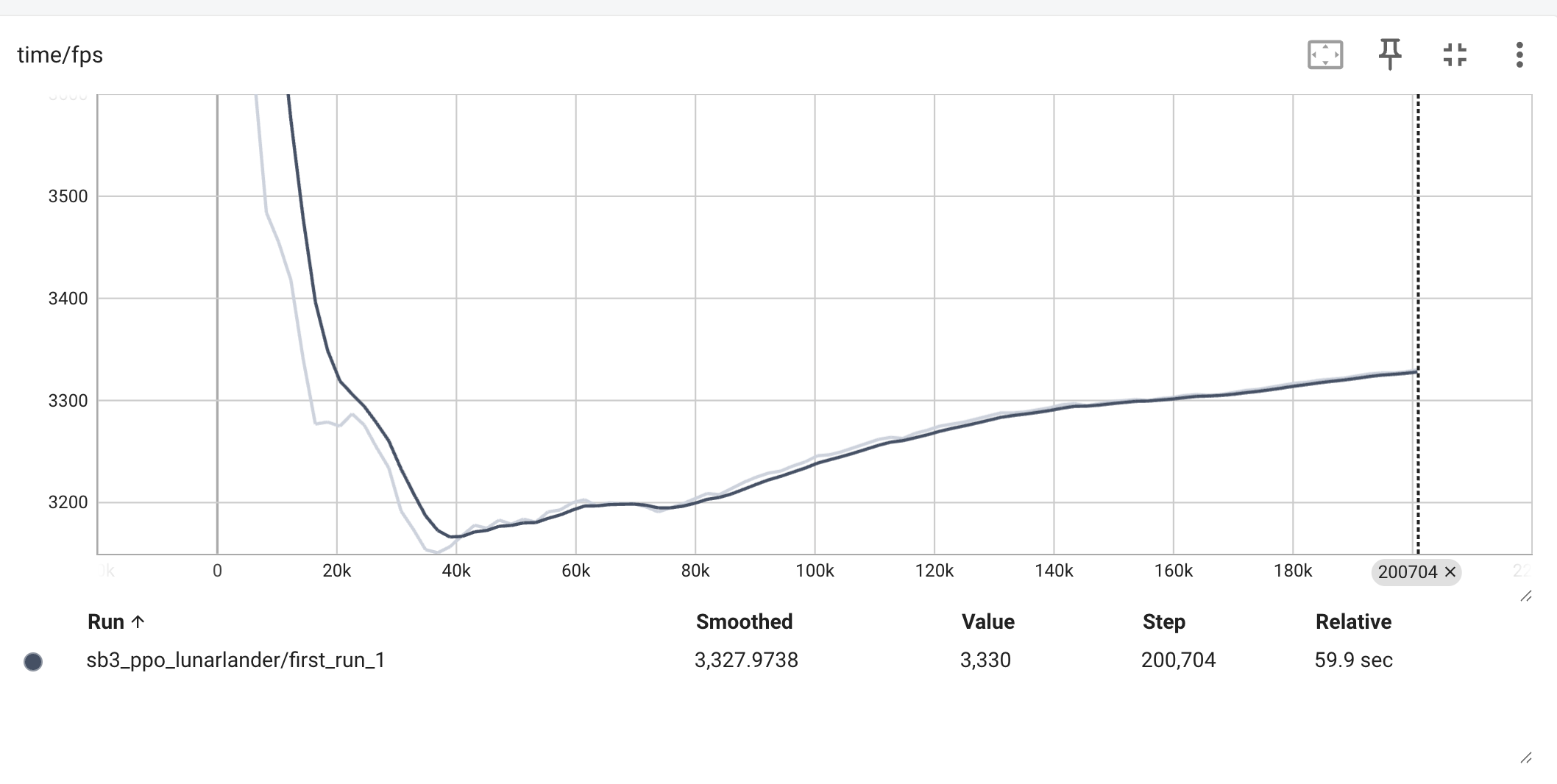
time/fps(每秒帧数):- 这个值主要反映了你的计算性能或训练速度。数值越高，训练得越快。
- 图中的曲线在短暂的初始波动后稳定在 3300 左右，说明训练速度是相当稳定的。
